零阶保持器的定义与作用:
零阶保持器:zero-order holder(ZOH),是指实现采样点之间插值的元件。零阶保持器基于时域外推原理,能够把采样信号转换成连续
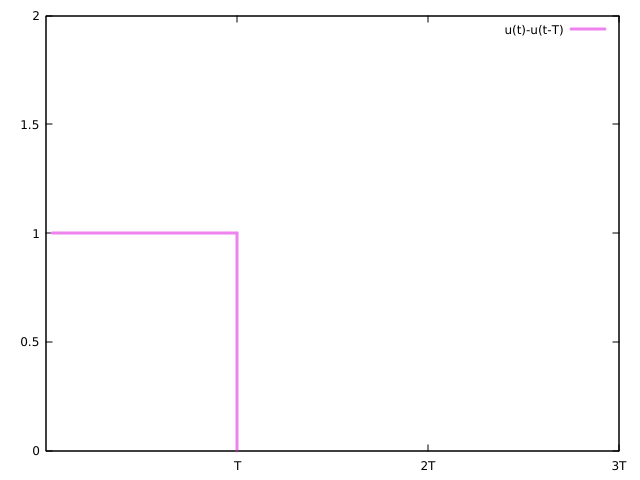
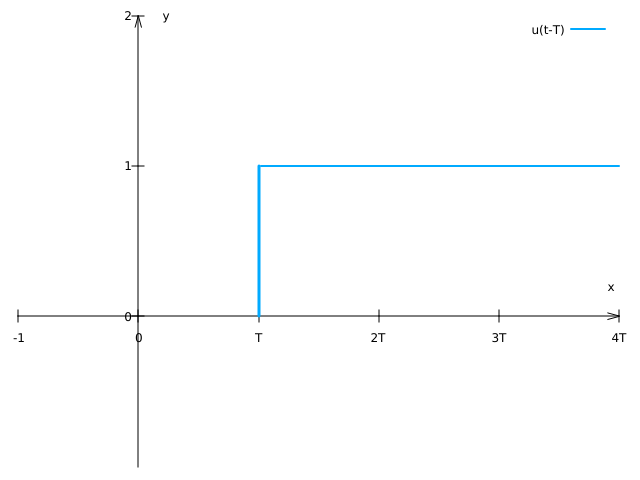
用阶跃信号u(t)减去另一个阶跃信号u(t-T)
根据傅里叶变换:
$ F(s) = \int_{-\infty}^{+\infty} f(t)e^{-st}dt $
对零阶保持器的时域表达式进行转换得:
$F(s) = \int_{-\infty}^{+\infty}{[u(t) – u(t-T)]} e^{-st}dt$
$ = \int_{-\infty}^{+\infty} u(t) e^{-st}dt – \int_{-\infty}^{+\infty}u(t-T)e^{-st}dt$
$ = \int_{0}^{+\infty} e^{-st}dt – \int_{T}^{+\infty} e^{-st}dt $
$ = (-\frac{1}{s} e^{-st}|^{+\infty}_{0}) – (-\frac{1}{s} e^{-st}|^{+\infty}_{T})$
$ = 0 – (-\frac{1}{s}) + 0 – \frac{e^{-sT}}{s} $
$ = \frac{1-e^{-sT}}{s} $
以上傅里叶变换其实可用其一些特性快速解决,不过为了保持逻辑的连贯性和揭露本质,直接用定义求解。
关于积分上下限分别是$(0, \infty)$和$ (T, \infty) $,是因为u(t)在t<=0时是没有值的,而u(t-T)在t<T没有值。两者图形如下(绘图的gnuplot命令见这篇文章:
接下来求解其Z变换, 由于系统是因果的,时间不存在小于0,应选用单边Z变换。
由于Z变换是针对离散序列,所以需要对阶跃函数离散化,用阶跃序列1(kT)表示,其中T是周期,k=1,2,3…表示第k个时间T, 函数能取到的值为1.
根据单边Z变换公式:
$ F(z) = \sum^\infty_{k=0} f(kT) z^{-k} $
可得阶跃序列的单边Z变换为:
$ F(z) = \sum^\infty_{k=0} 1(kT) z^{-k} = \sum^\infty_{k=0} z^{-k} $
根据等比数列求和公式,可得上式:
$ = \frac{1-z^{-k}z^{-1}}{1-z^{-1}} $
$ = \frac{z-\frac{1}{z^k}}{z-1} $
当$|z|>1$时,$ lim_{k\to \infty} = 0 $, 上式可化简为:
$ F(z) = \frac{z}{z-1}$ $ |z| > 1 $
同理,u(t-T)对应的离散序列u(kT-T)的单边Z变换为$ F(z) = \frac{1}{z-1}$
$ \rightarrow $ 零阶保持器的单边Z变换为 :
$ \frac{z}{z-1} – \frac{1}{z-1} = 1$
为什么是1呢?
因为, 输入的采样信号是离散的,零阶保持器的时域函数在时间T以前的离散化只有一个值,位于0点,是一个冲激函数,而且不能改变输入的幅值,所以为1。
不过,求取这个没有多少意义,只是让我们知道了这是对应了实际意义的,在一般求解的过程中要计算零阶保持器s传递函数乘于执行结构的s传递函数再求二者乘积的Z变换。